The rate of reaction having collision frequency Z and fraction f of molecules will be:
Rate of reaction = – dx / dt = Z x f
The collision frequency Z and fraction f of molecules varies with temperature and affects the rate of reaction is discussed below:
1. Collision frequency (Z):
With increase in temperature, the average velocity of the molecules increases and therefore the collision frequency i.e. number of collisions per second per unit volume also increases. But it is known that the collision frequency is directly proportional to the square root of the absolute temperature. Hence the ratio of the collision frequency at 298 K and 308 K will be given by:
Z308 / Z298 = (308 / 298) 1/2 = 1.016
Hence, if the increase in the rate of reaction with increase in temperature were due to increase in collision frequency, the rate should increase only by 1.016 times with 100 rise in temperature. However the actual increase is two times or even more. This means that the increase in the rate of reaction with increase in temperature is not due to increase in collision frequency alone.
2. Fraction (f) of molecules having effective collisions:
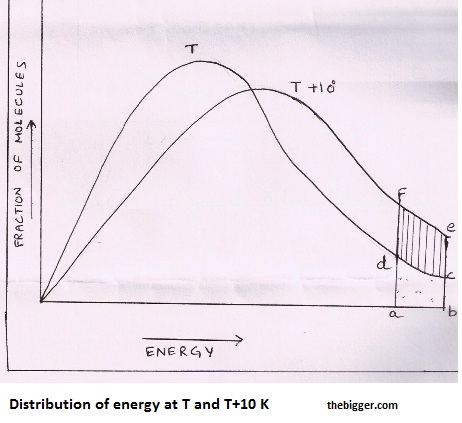
For a collision to be effective, the colliding molecules must have energy more than threshold energy. At a particular temperature T, if fractions of molecules are plotted versus corresponding energies, a graph of the type shown in fig. 1 is obtained. If the point ‘a’ represents threshold energy, the shaded area abcd represents the fraction of molecules having energy greater than threshold value.
When the temperature is increased to T + 100, the curve shifts as shown in fig. 1. Now the fraction of molecules having energy greater than threshold value is represented by the shaded area abef which is almost double than the area abcd. Thus the increase in the rate of reaction with increase in temperature is mainly due to increase in the number of effective collisions.